Wenn Sie die einzelnen Lösungs-Schritte in das Sudoku-Raster der Ausgangssituation von Erklärungs-Beispiel 1 eingetragen haben, sind Ihnen bestimmt die nächsten Lösungen auch eingefallen, mindestens bei den Schritten 3., 8. und 10. als jeweils nur noch eine letzte fehlende Ziffer in einen Quadranten oder eine Spalte einzutragen waren.
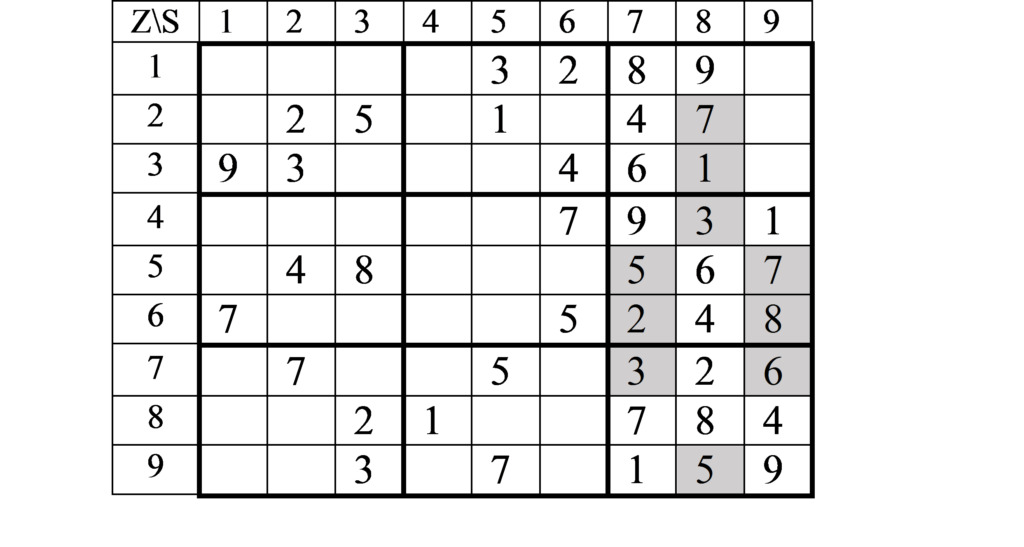
Aber vielleicht, und, wenn Sie schon ein erfahrener Sudoku-Fan sind, ganz sicher sogar, haben Sie auch gesehen, dass und warum in Schritt 1. eine „5“ in das Feld „IX h“ also im Quadranten unten rechts in das Feld unten in der Mitte eingetragen werden kann.
In Quadrant IX sind in der Ausgangssituation nur noch drei Felder frei, es fehlen hier noch die Ziffern „3“, „5“ und „6“. Und die „5 nebenan“, in „5“ Quadrant VIII blockiert die zwei freien Felder in Zeile 7 im Quadranten IX für die in diesem Quadranten noch fehlende „5“. Deshalb kann diese nur in Feld „IX h“ stehen (1. IX h 5).
Und, wenn die fehlende „5“ in Quadrant IX eingetragen ist, fehlen nur noch die „3“ und die „6“ in diesem Quadranten.
Und weil in Quadrant III (oben rechts) schon eine „6“ eingetragen ist (in Feld III g), kann die „6“ in Quadrant IX nur in Feld „c“ stehen (2. IX c 6).
Und jetzt fehlt nur noch eine Ziffer in Quadrant IX, die „3“, ihre Position ergibt sich nun völlig automatisch im letzten freien Feld (3. IX a 3).
Das ist eine wahrhaft einfache Lösung und führt zu
Regel 1: Die einfachen Lösungen suchen
Immer, wenn sich eine einfache Ergänzung ergibt, weil irgendwo in einer Zeile oder Spalte oder in einem Quadranten nur noch ein freies Feld ist, tragen Sie die fehlende Ziffer ein.
Damit ist diese Aufgabe erledigt und das Raster füllt sich weiter. Viel wichtiger noch: dieses einfach auszufüllende Feld gibt Ihnen (vielleicht) wichtige Hinweise für weitere Lösungen, z.B. weil jetzt ein Feld weniger frei ist (wie oben in unserem Beispiel für die „2“ und die „5“, die jetzt nur noch in Spalte 7 fehlen) und leicht zur nächsten Lösung führt (hier zum Eintragen der „5“) – und danach, wieder eine „einfache Lösung“ nach Regel zum Eintragen der „2“ als letzter fehlender Ziffer in Spalte 7.
Diese Logik führt zu
Regel 2: Da weiter machen, wo Einträge erfolgt sind
Für unser kleines Beispiel heißt dies:
Wenn wir in Schritt 1. die „5“ in Feld „IX h“ eingetragen haben, machen wir da weiter.
Was kann denn „da“ im Sinne dieser Regel 2 bedeuten?
Nun, das Feld „IX h“ gehört zu Quadrant IX, Zeile 9 und Spalte 8. Und diese drei Regionen auf dem Sudoku-Spielfeld sind geeignet um dort nach weiteren Lösungen zu suchen. So wie wir es im zweiten Lösungsschritt gemacht haben, nachdem wir die „5“ in Quadrant IX eingetragen haben. Wir haben in Quadrant IX nach weiteren Lösungen gesucht.
Die konsequente Anwendung von Regel 2 (Da weiter machen, wo Einträge erfolgt sind) kann oft zu einer schönen (und relativ einfachen) Kette von weiteren Lösungen führen. Der Grund dafür ist, dass sich mit jedem weiteren Eintrag in einer Zeile oder Spalte oder einem Quadranten die Anzahl der verbleibenden Felder und Möglichkeiten in diesem Gebiet reduziert.
In unserem kleinen Beispiel sind die Lösungen in Schritt 2., 4., 5., 6., 7., 9. Anwendungen dieser Regel.
Manchmal allerdings (und je schwieriger die Rätsel sind, desto häufiger) gibt es keine einfache und offensichtliche „nächste“ Lösung. Auch am Anfang eines Sudokus gibt es noch keine gerade erfolgten Einträge bei denen man einfach nur weiter machen muss.
Am Anfang eines Sudokus und mittendrin, wenn die Suche nach weiteren, relativ einfachen Lösungen „stockt“ helfen uns die weiteren Regeln 3, 4, 5 und 6, die wir auch noch kennenlernen werden.
Ein guter Start ist es oft, wie in unserem kleinen Beispiel von eben, wenn man dort sucht, wo schon viele Einträge vorhanden sind (hier war das Quadrant IX mit schon sechs vorhandenen Einträgen).
Mein Tipp: Schauen Sie sich zu Beginn eines Sudokus kurz die schon vorgegebenen Einträge an und verschaffen sich einen Überblick.
Wo gibt es schon vier oder fünf oder sogar sechs Einträge in einem Quadranten oder einer Spalte oder einer Zeile?
Dieser Tipp führt zu
Regel 3: Viele vorhandene Einträge suchen
Diese Regel lässt sich nicht nur sehr gut auf Quadranten, Zeilen und Spalten anwenden, sondern, sozusagen als Variante, auch auf die Anzahl der eingetragenen Ziffern selbst.
Auch hierzu ein kleines Beispiel, diesmal für ein „schwieriges“ Sudoku:
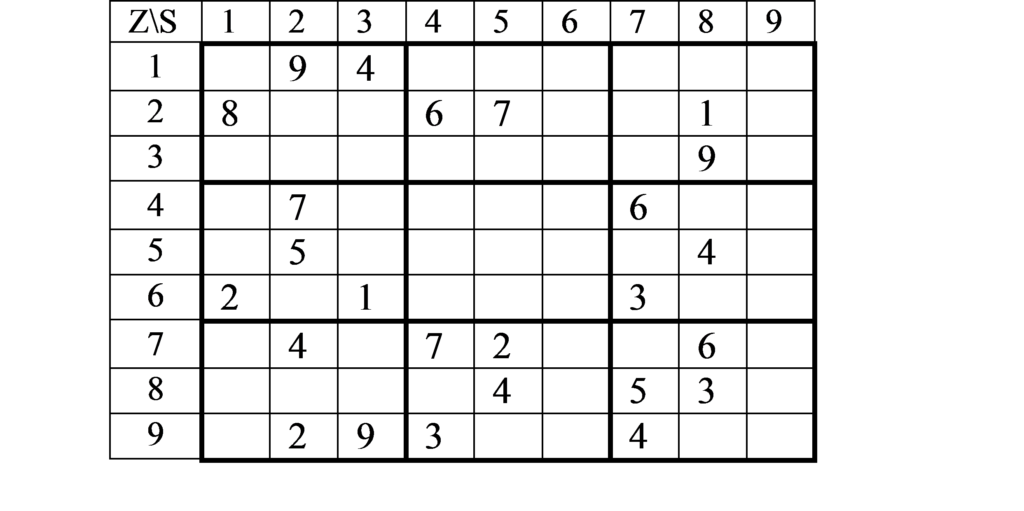
Der eben angesprochene Überblick, den Sie sich zu Beginn verschaffen sollten, könnte zum Beispiel so aussehen:
„Der zentrale Quadrant V ist völlig leer. Es wird interessant sein zu beobachten, wie er sich füllt. Andere Quadranten sind besser gefüllt: IV, VIII und IX mit je vier Einträgen. Spalte 2 und 8 weisen sogar fünf Einträge auf. Auch die Ziffer „4“ ist fünf Mal eingetragen.“
Aha, also finden wir hier schon schöne Hinweise auf eine
mögliche Anwendung von
Regel 3: Viele vorhandene Einträge suchen
Und an diesem Beispiel lassen sich die beiden Varianten von Regel 3 schön erläutern.
Zunächst schauen wir uns die vielen Einträge in Spalte 2 einmal näher an:

Es fehlen in Spalte 2 noch die Ziffern „1“, „3“, „6“ und „8“.
Finden wir irgendwo Informationen zu diesen fehlenden Ziffern? Oh ja und zwar gleich in Zeile 2: dort „blockieren“ die eingetragenen Ziffern „1“, „6“ und „8“, dass diese Ziffern in das Feld „I e“ eingetragen werden können. Das heißt: in „I e“ kann nur eine „3“ stehen!
Die andere Variante von Regel 3 führt zu den fünf Einträgen von Ziffer „4“:

In den drei unteren Quadranten VII, VIII und IX ist die „4“ schon eingetragen, daraus können wir kaum zusätzliche Informationen über die noch fehlenden Einträge für eine „4“ finden.
Schauen wir jedoch auf die „4“ in Quadrant I und VII sieht die Sache schon ganz anders aus. Die Einträge in diesen beiden Quadranten schließen viele Möglichkeiten für ein Eintragen der „4“ im dazwischen liegenden Quadranten IV aus. Das kann man sich so veranschaulichen:
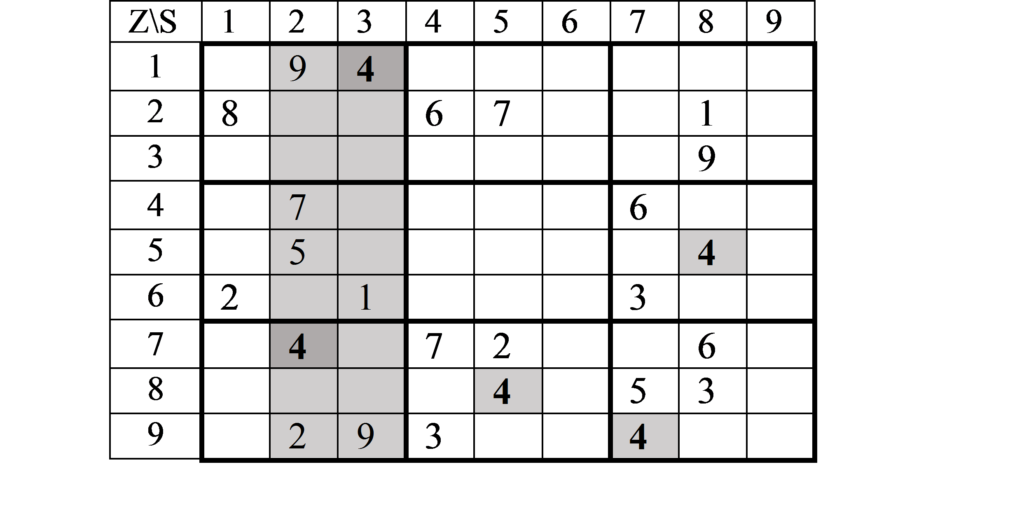
Die beiden eingetragenen „4“ in Spalte 2 und 3 blockieren diese für eine weitere Eintragung einer „4“ in diesen Spalten. Die dadurch ausgeschlossenen Felder sind hier grau unterlegt. Also kann in Quadrant IV in den Feldern IV c, IV f und IV h keine „4“ stehen. Es bleiben nur noch zwei Möglichkeiten für die „4“ in Quadrant IV, nämlich Feld a und d.
Schauen wir, ob wir Informationen finden können, ob in diesen Feldern eine „4“ stehen kann.
Bingo! Durch die in Quadrant VI in Feld „e“ eingetragene „4“ kann keine weitere „4“ in Zeile 5 stehen.
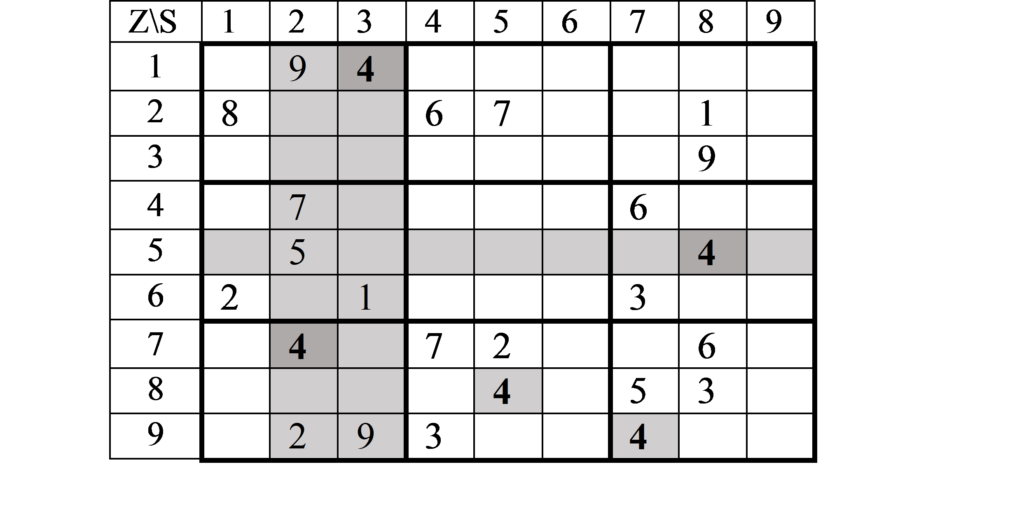
Also bleibt in Quadrant IV nur Feld „a“ für die „4“:

Fassen wir kurz zusammen:
Ein Sudoku-Spielfeld lässt sich einteilen in Spalten, Zeilen, Quadranten und Felder, die wir kurz bezeichnen können, damit wir über Sudoku-Lösungen schreiben und sprechen können.
„S2“ bezeichnet Spalte 2, „Z4“ bezeichnet Zeile 4, „VII“ bezeichnet den siebten Quadranten, also den ersten von links in der dritten Reihe oder anders ausgedrückt den Quadranten „unten links“.
Die Feldbezeichnung „VII a“ bezeichnet das erste Feld (oben links) in Quadrant VII.
Usw.
Für das Finden von Lösungen für ein Sudoku haben wir bisher hierher drei Regeln kennengelernt:
Regel 1 Die einfachen Lösungen suchen
Regel 2 Da weiter machen, wo Einträge erfolgt sind
Regel 3 Viele vorhandene Einträge suchen
Diese drei Regeln reichen oft schon aus um einfache Sudokus vollständig zu lösen!
Und sie stellen die Basis-Regeln dar für die Lösung von schwierigeren Sudokus.
Für die Lösung von diesen schwierigen Sudokus benötigen wir noch drei weitere Regeln, die mit Videos und Erklärungen im Mitgleider-Bereich erläutert werden.
zurück